南昌工程学院是2020年江西省招生院校之一。2020年南昌工程学院文化管理专业微积分该考什么？我们来看看南昌工程学院2020年微积分考试大纲。

南昌工程学院2020年《微积分》考试大纲

(a)考试大纲的一些注释:

1.《微积分》是金融与管理专业后续经济数学和专业课的基础，是教学计划中的核心基础课。

2.考试要求和性质南昌工程学院微积分考试是一项具有选择性的水平考试，其目的是选拔优秀的专科生来我校学习。因此，这门课程的考试既需要知识评估，也需要能力评估。因此，考生在复习这门课程时，应注意系统掌握本大纲规定的基本知识和技能，提高计算能力，发展逻辑思维能力，应用数学知识分析和解决实际问题。

3.本大纲要求由低到高，概念和理论分为“理解”和“认识”两个层次；方法和操作分为“知道”、“掌握”、“掌握”三个层次。

4.本课程考试方式封闭:答题时间120分钟:分数以百分制为准；考试内容是本大纲规定的“考核知识点”和“考核目标与基本要求”的内容，试题难度按照易、中、难三级比例为30:50:20。

5.问题①填写空题:共5道小题，每道小题4分，每道小题20分。②单项选择题(四个备选答案中，只有一个是正确的):小题5个，每个小题4分，每个小题20分。③答案(含证明题):共6题，60分。

6.参考教材:《经济应用数学》，哈尔滨工程大学屠青主编

(二)考试内容和各知识点的具体要求

一、函数、极限和连续性

(a)职能

1.知识范围

(1)函数的概念函数的定义、函数的表示、分段函数和隐函数。

(2)函数的性质是单调性、宇称性、有界性和周期性。

(3)反函数的定义和反函数的形象

(4)基本初等函数幂函数、指数函数、对数函数、三角函数、反三角函数。

(5)函数的四次运算和复合运算

(6)初等函数

(7)共同的经济职能

2.要求

(1)理解函数的概念。会找到函数的表达式，定义域，函数值。会找到分段函数的定义域和函数值，会做出分段函数的简单图像。

(2)了解函数的单调性、奇偶性、有界性和周期性。

　　(3)了解函数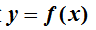专升本考试大纲(微积分)" alt="2020南昌理工学院专升本考试大纲(微积分)" width="96" height="30" border="0" vspace="0" style="width: 96px; height: 30px;"/>(3)了解功能

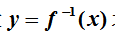与其反函数专升本考试大纲(微积分)" alt="2020南昌理工学院专升本考试大纲(微积分)" width="115" height="37" border="0" vspace="0" style="width: 115px; height: 37px;"/>(定义域、值域、镜像)之间的关系，就会找到单调函数的反函数。(4)掌握函数的四则运算和复合运算。

(5)掌握基本初等函数及其图像的性质。

(6)理解初等函数的概念。

(7)建立简单实际问题的函数关系(需求函数、供给函数、成本函数、效益函数、利润函数)。

(2)限制

1.知识范围

(1)数列极限数列的概念，数列极限的定义

(2)数列极限的性质:唯一性、有界性、四个算法、pinching定理、单调有界数列极限存在定理。

(3)函数极限的概念函数极限在一点上的定义，左极限和右极限及其与极限的关系，函数极限趋近于无穷大时的情况，函数极限的几何意义

(4)函数极限的唯一性，四个算术规则，pinching定理。

(5)无穷小量和无穷小量的定义，无穷小量和无穷小量的关系，无穷小量和等价无穷小量的性质。

(6)两个重要的限制

2.要求

(1)理解极限的概念。求一个函数在一点的左右极限，了解极限在一点存在的充要条件。

(2)了解极限的相关性质，掌握极限的四种算法。

(3)理解无穷小量的概念，掌握无穷小量的性质和无穷小量与无穷小量的关系。将进行无限阶(高阶、低阶、同阶和等价)的比较。掌握极限的收敛准则，你会用等价无穷小量来代替求极限。

(4)掌握用两个重要极限求极限的方法。

(3)连续性

1.知识范围

(1)函数连续性的概念函数在一点上的连续性、左连续性和右连续性、函数在一点上的定义

函数连续、不连续点及其分类的充要条件。

(2)函数在一点上连续的性质连续函数的四种运算，复合函数的连续性和反函数的连续性

(3)闭区间上连续函数的有界性定理、最大最小值定理、中值定理(包括零点定理)。

(4)初等函数的连续性

2.要求

(1)理解函数在一点上的连续性和不连续性的概念，理解函数在一点上的连续性与极限存在性的关系，掌握判断函数(包括分段函数)在一点上的连续性的方法。

(2)会发现函数的不连续性，确定其类型。

(3)掌握闭区间上连续函数的性质，一些简单的命题会被中值定理证明。

(4)为了理解初等函数在其定义区间内的连续性，我们将利用连续性来寻找极限。

二、一元函数微分学

(a)导数和微分

1.知识范围

(1)导数、左导数和右导数的定义，函数在一点可导的充要条件，导数的几何和物理意义，可导与连续的关系。

(2)求导法则和求导的基本公式，求导的四种运算，反函数的求导，求导的基本公式。

(3)求导法复合函数求导法，隐函数求导法，对数求导法，参数方程确定的函数求导法，分段函数求导法。

(4)高阶导数的定义和简单计算。

(5)微分的定义，微分与导数的关系，微分法则，一阶微分形式的不变性。

2.要求

(1)了解导数的概念及其几何意义，了解可导性与连续性的关系，掌握通过定义求一个函数在一点的导数的方法。

(2)将得到曲线上某一点的切线方程和法向方程。

(3)掌握导数的基本公式、四大算术规则以及复合函数的求导方法，就会得到反函数的导数。

(4)掌握隐函数求导法、对数求导法、参数方程确定的函数求导法，可以求出分段函数的导数。

(5)理解高阶导数的概念，会发现简单函数的N阶导数。

(6)理解函数微分的概念，掌握微分的基本公式和算法，理解可微性和可微性的关系，求函数的一阶微分。

(二)微分中值定理及其导数的应用

1.知识范围

(1)微分中值定理罗尔定理和拉格朗日中值定理。

(2)洛杉矶医院法

(3)判断功能增减的方法

(4)函数的极值和极值点的最大值和最小值

(5)曲线和拐点的凹凸性

(6)曲线的水平渐近线和垂直渐近线

(7)导数在经济中的应用

2.要求

(1)了解罗尔定理、拉格朗日中值定理及其几何意义。会用罗尔定理证明方程根的存在性。会用拉格朗日中值定理证明简单不等式。

(2)掌握用洛必达定律求待定公式极限的方法。

(3)掌握用导数判断函数单调性的方法，求出函数的单调递增和递减区间，将利用函数的单调性证明简单不等式。

(4)理解函数极值的概念。掌握求函数极值、最大值、最小值的方法，会解决简单的应用问题。

(5)会判断曲线的凹凸性质，找到曲线的拐点。

(6)将得到曲线的水平渐近线和垂直渐近线。

(7)可以制作简单功能的图形。

(8)会做边际分析和弹性分析。

3.一元函数的积分学

(a)不定积分

1.知识范围

(1)不定积分原函数和不定积分的定义，原函数的存在定理和不定积分的性质。

(2)基本积分公式

(3)靠前种代换法(微分法)和第二种代换法的转换积分法

(4)部分集成

(5)一些简单有理函数的积分

2.要求

(1)理解原函数与不定积分的概念和关系，掌握不定积分的性质，理解原函数的存在定理。

(2)掌握不定积分的基本公式。

(3)掌握不定积分的靠前种代换方法，掌握第二种代换方法(限于三角代换和简单根式代换)。

(4)掌握不定积分的分部积分。

(5)可以得到简单有理函数的不定积分。

(2)定积分

1.知识范围

(1)定积分的概念，定积分的定义，它的几何意义和可积条件

(2)定积分的性质

(3)分部积分变上限的定积分牛顿-莱布尼茨公式的计算

(4)无限区间的广义积分

(5)定积分的应用平面图形的面积，旋转体的体积，物体沿直线运动时变力所做的功。

2.要求

(1)理解定积分的概念，掌握定积分的几何意义，理解函数的可积条件。

(2)掌握定积分的基本性质。

(3)了解变上限积分是变上限的函数，掌握变上限定积分求导的方法。

(4)掌握牛顿-莱布尼茨公式。

(5)掌握转换积分法和定积分的分部积分。

(6)理解无穷区间广义积分的概念，掌握其计算方法。

(7)掌握直角坐标系中定积分计算的平面图形面积，以及平面图形绕坐标轴旋转产生的旋转体体积。会用定积分解决一些简单的经济问题。

四、多元函数微分学

1.知识范围:

(1)多元函数的概念和二元函数的极限；

(2)多元函数的偏导数和全微分的概念，以及全微分的计算

(3)多元函数极值和条件极值的概念，求函数极值，二元函数极值存在的必要条件和二元函数极值存在的充分条件，拉格朗日乘数法

2.要求:

(1)理解多元函数的概念，二元函数的极限和连续性的概念，求二元函数的定义域

(2)理解偏导数的概念，掌握二元函数一阶和二阶偏导数的计算方法

(3)会求二元函数的全微分，会求多元复合函数和隐函数的偏导数

(4)掌握二元函数的极值。

部分内容来源于网络转载、学生投稿，如有侵权或对本站有任何意见、建议或者投诉，请联系邮箱（1296178999@qq.com）反馈。 未经本站授权，不得转载、摘编、复制或者建立镜像， 如有违反，本站将追究法律责任！

本文标签： 江西专升本

上一篇：2020南昌理工学院专升本英语考试大纲                  下一篇：2020南昌理工学院专升本考试大纲(高级英语)